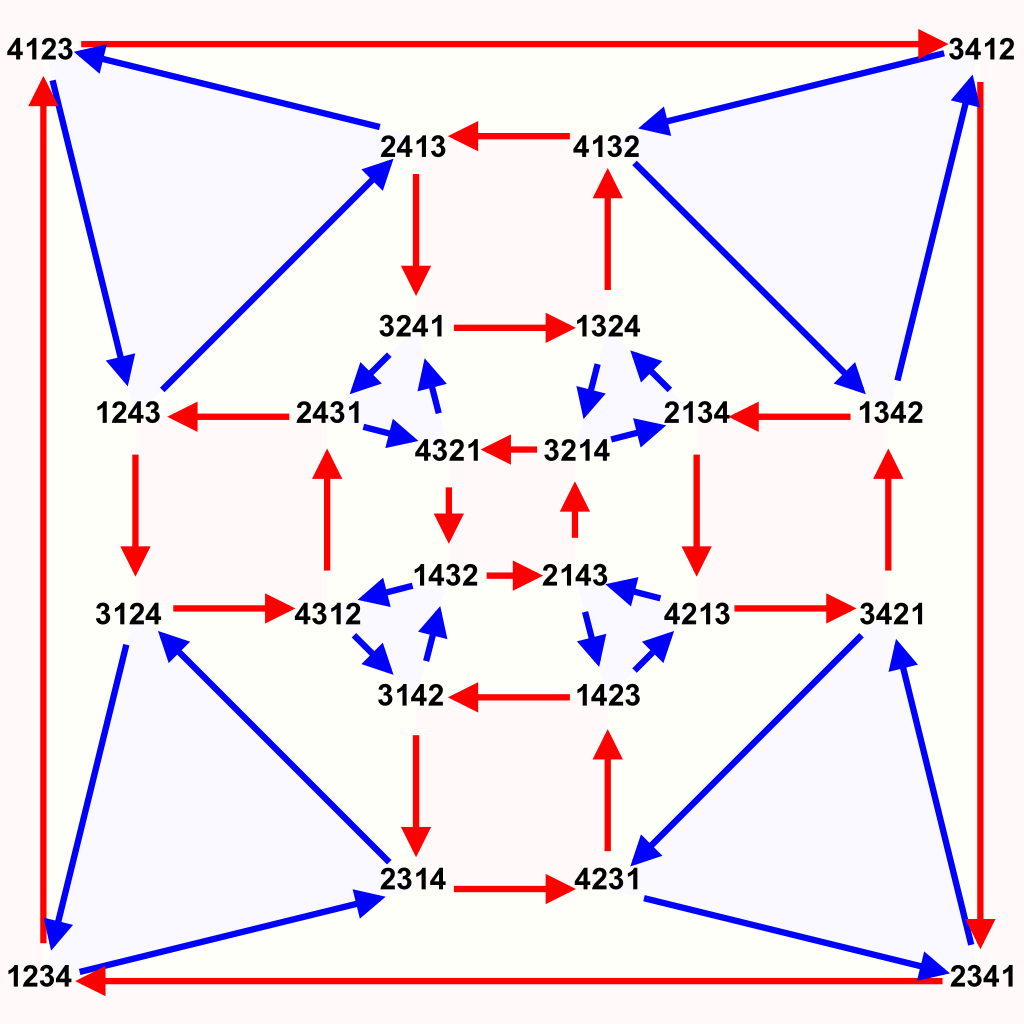
집합 G에서 정의된 연산 $\cdot$이 아래를 공리를 만족하면 집합 G는 연산 $\cdot$에 대하여 군(群: group)을 이룬다고 말한다. 군 $(G, \cdot )$로 적는다.
결합법칙 Associativity
모든 $a,b,c \in G$에 대하여 $(a\cdot b)\cdot c=a\cdot (b\cdot c)$를 만족한다.
항등원 Identity element
모든 $a\in G$에 대하여 $a\cdot e=e \cdot a=a$를 만족하는 원소 $e \in G$가 존재한다.
역원 Inverse element
모든 $a \in G$에 대하여 $a\cdot b=b\cdot a =e$를 만족하는 $ b \in G$가 존재한다.
교환법칙까지 된다면 교환군(commutative group) 또는 아벨군(abelian group)이다.