호도법

육십분법은 원 둘레를 360등분 했을 때 잘린 부채꼴 하나의 중심각을 $1^o$로 쓰는 것이다. 그런데 숫자로 같은 1이라고 쓰지만 길이에서 쓰는 $1$과 다르다. 다르게 이야기하면 육십분법으로 적은 수는 실수가 아니다. 이제 각을 길이로 나타내 보자.
1라디안은 반지름과 호의 길이가 같은 부채꼴의 중심각의 크기다.
이렇게 하면 각을 길이로 재는 것이 되므로 각의 크기가 실수가 된다. 따라서 각을 나타내는 단위를 쓰지 않아도 된다. 실수에서 실수로의 함수를 정의하기 위해 피할 수 없다. 처음엔 어려워 보이지만 각을 라디안으로 나타내는 것이 훨씬 편하다. 반지름이 $r$이고 중심각이 $180^o $인 부채꼴은 호의 길이가 $\pi r$이므로 아래와 같은 육십분법과 호도법 사이의 관계를 얻는다.
$$180^o =\pi(radian)$$
http://en.wikipedia.org/wiki/Radian
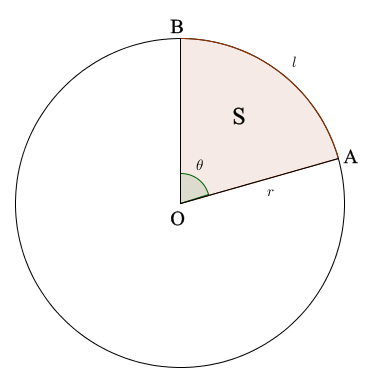
호도법으로 각을 나타내면 모든 것이 간단해진다. 반지름의 길이가 $r$, 중심각 크가가 $\theta$인 부채꼴 $OAB$에서 호 $AB$의 길이를 $l$, 넓이를 $S$라고 하자. 호의 길이와 넓이는 모두 중심각에 비례한다.
$$l:2\pi r =\theta:2\pi$$
$$\therefore \; l=r\theta$$
$$S:\pi r^2 =\theta:2\pi$$
$$\therefore\;S=\frac{1}{2}r^2 \theta=\frac{1}{2}rl$$

