$a>0,\;\;a\not= 1$일 때, $a^x=b$를 만족하면 $x$를 $a$를 밑으로 하는 $b$의 로그라고 하고 $x= \log_a b$라고 적는다.
로그를 처음으로 고안한 네이피어가 사용한 방정식은 아래와 같다.
$$N=10^7 (1-10^{-7})^L$$
네이피어는 처음에 L을 "인공수"(artificial number)라고 부르다가 비율을 의미하는 "로그"(logarithm)라는 이름으로 소개했다. 그리스어 λόγος(logos)는 '부분'을 의미하며, ἀριθμός(arithmos)는 '숫자'를 뜻한다. 현대적 표현법으로 나타낸 자연로그와의 관계는 다음과 같다.
$$L=\log_{1-10^{-7}} \frac{N}{10^{7}}\approx 10^7 \log_{\frac{1}{e}}\frac{N}{10^{7}}\approx -10^7 \log_{e}\frac{N}{10^{7}}$$
https://ko.wikipedia.org/wiki/지수(수학)
로그 (수학) - 위키백과, 우리 모두의 백과사전
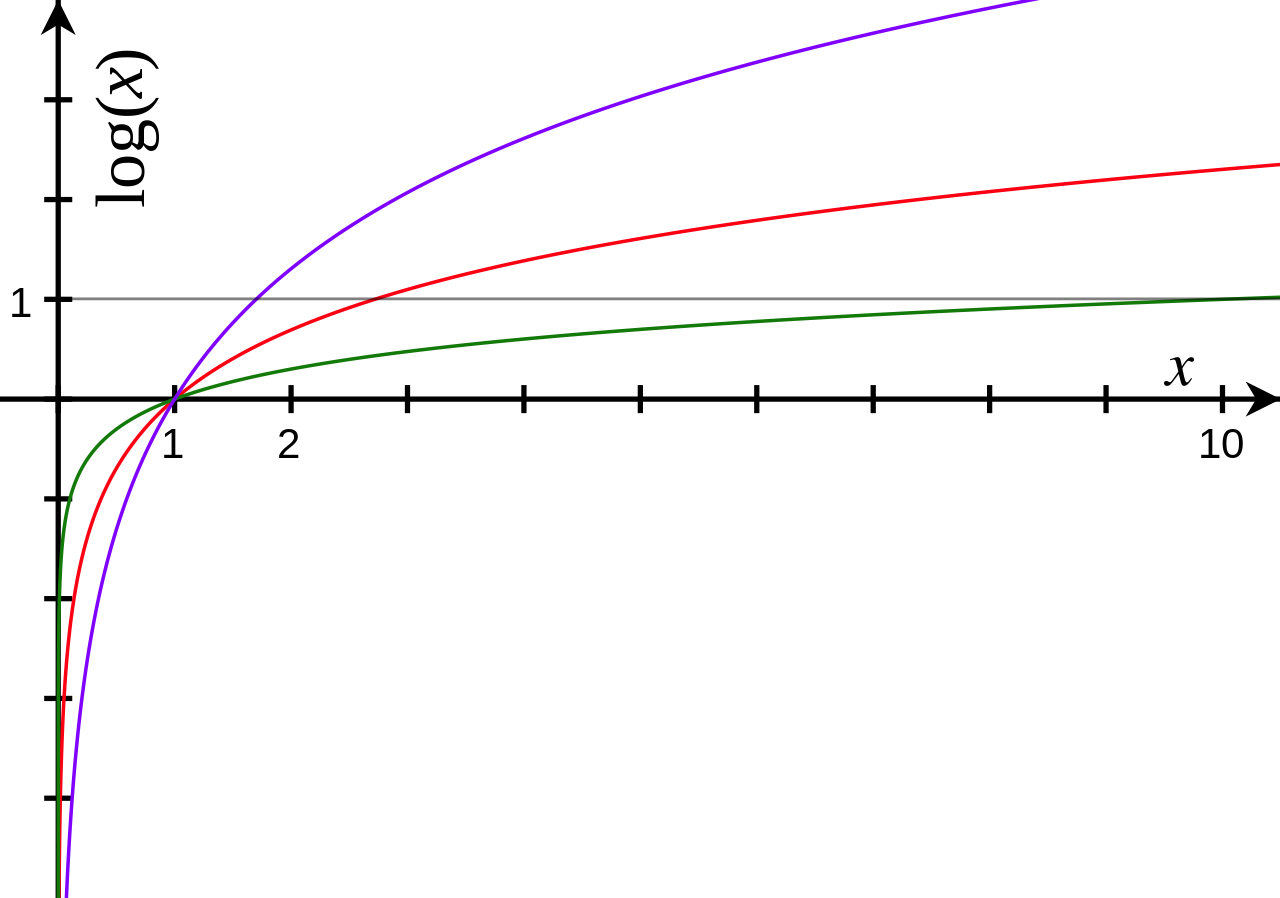
위키백과, 우리 모두의 백과사전. 다양한 로그 곡선. 붉은 색은 밑이 e, 초록색은 밑이 10, 보라색은 밑이 1.7이다. 밑 값에 상관없이 모든 로그곡선은 (1, 0)을 지난다. 로그(log)는 지수 함수의 역함
ko.wikipedia.org

