서로 외접하는 원이 있을 때 바깥에 있는 원이 안쪽에 있는 원과 접하면서 구른다고 하자. 이 때 바깥 원 위에 있는 한 정점이 그리는 자취가 에피사이클로이드 곡선이다.

두 원의 반지름을 각각 $R$, $r$이라 하자. 이 곡선은 두 원의 반지름이 이루는 비 $k$ $(R=kr)$에 따라 아래와 같은 모양이 된다.
 |
 |
 |
 |
 |
 |
 |
 |
이제 방정식을 구해보자.
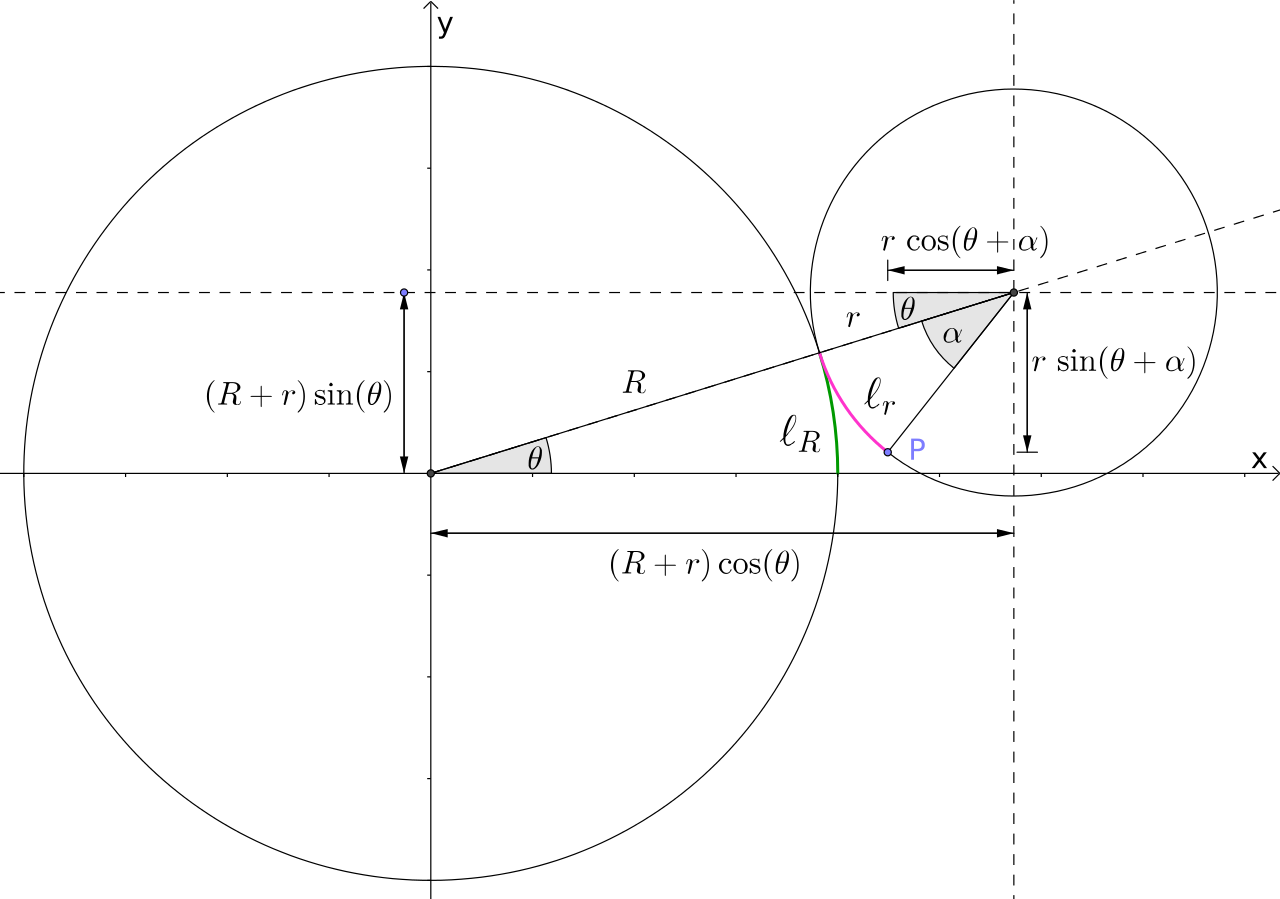
$$l_R=R\theta=r\alpha=l_r$$
$$\alpha=\frac{R\theta}{r}$$
점 $P$의 좌표 $(x(\theta),y(\theta))$는 아래와 같이 매개변수를 써서 나타낼 수 있다.
$$x(\theta)= (R+r)\cos\theta-r\cos(\theta+\alpha) = (R+r)\cos\theta-r\cos\bigg(\frac{R+r}{r}\bigg) \theta$$
$$y(\theta)= (R+r)\sin\theta-r\sin(\theta+\alpha) = (R+r)\sin\theta-r\sin\bigg(\frac{R+r}{r}\bigg) \theta$$
또는 $k$를 써서
$$x(\theta)= r(k+1)\cos\theta-r\cos(k+1) \theta$$
$$y(\theta)= r(k+1)\sin\theta-r\sin(k+1) \theta$$
로 적을 수 있다.
$k$가 자연수일 때, 이 곡선의 길이 $L$을 구해보자.
먼저
$$\frac{dx}{d\theta}= -r(k+1)\sin\theta+r(k+1)\sin(k+1) \theta$$
$$\frac{dy}{d\theta}= r(k+1)\cos\theta-r(k+1)\cos(k+1) \theta$$
$$\bigg(\frac{dx}{d\theta}\bigg)^2= r^2(k+1)^2 (\sin\theta-\sin(k+1) \theta)^2$$
$$\bigg(\frac{dy}{d\theta}\bigg)^2= r^2(k+1)^2(\cos\theta-\cos(k+1) \theta)^2$$
$$\bigg(\frac{dx}{d\theta}\bigg)^2+\bigg(\frac{dy}{d\theta}\bigg)^2 =r^2(k+1)^2(2-2\cos k \theta)= 2^2 r^2 (k+1)^2 \sin^2 \bigg(\frac{k}{2}\theta\bigg)^2$$
두 뾰족점 사이 거리를 $l$이라 하면 $L=kl$이다.
$$\begin{split}l&=\int_{0}^{2\pi/k}\sqrt{\bigg(\frac{dx}{d\theta}\bigg)^2+\bigg(\frac{dy}{d\theta}\bigg)^2}d\theta\\&= \int_{0}^{2\pi} 2 r (k+1) \sin \bigg(\frac{k}{2}\theta\bigg)d\theta\\&=2r(k+1)\bigg[-\frac{2}{k}\cos\bigg(\frac{k}{2}\theta\bigg)\bigg]_{0}^{2\pi/k}\\&=8r\frac{k+1}{k}\end{split}$$
그러므로 $L=8r(k+1)=8(R+r)$이다.



